Einfaldar og ódýrar eðlisfræðitilraunir

Ég er að vinna verkfeni fyrir þróunarsjóð námsgagna. Hér mun ég uppfæra það sem komið er jafn óðum.

Hlaða síma

Tækjabúnaður:

• Sími
• Leið til að hlaða símann
• Skeiðklukka

Þetta er afar einföld tilraun sem að þarfnast einungis tíma – ekki hægt að gera þessa í hefðbundinni kennslustund.

Lýsing

Hlaðið síma frá 0% í 100%. Tíminn sem þetta tekur fer eftir hleðslutækinu og símanum sem að þið notið. Í mínu tilviki tók þetta rúmar tvær klukkustundir. Hugsanlega hægt að ná þessu neðar með minni rafhlöðum (eldri símum) og/eða hraðari hleðslu. Skráið hjá ykkur með nokkuð jöfnu millibili hleðsluna á símanum sem fall af tíma.

Mæliniðurstöður og úrvinnsla

Hér eru mæliniðurstöðurnar mínar og úrvinnsla:

Tími [mín]	Hleðsla [%]
1.33	2
2.33	3
4.00	4
10.97	8
17.50	14
19.50	17
23.50	22
26.33	25
31.28	31
32.50	33
34.67	35
38.42	39
42.00	43
43.73	45
46.75	49
48.67	51
51.50	53
52.98	56
57.03	61
65.00	68
69.95	71
74.63	75
77.42	77
81.30	80
83.75	82
86.88	85
89.50	87
94.08	90
96.85	92
99.73	93
101.35	94
104.85	95
108.08	97
111.35	98
114.43	99
118.58	100

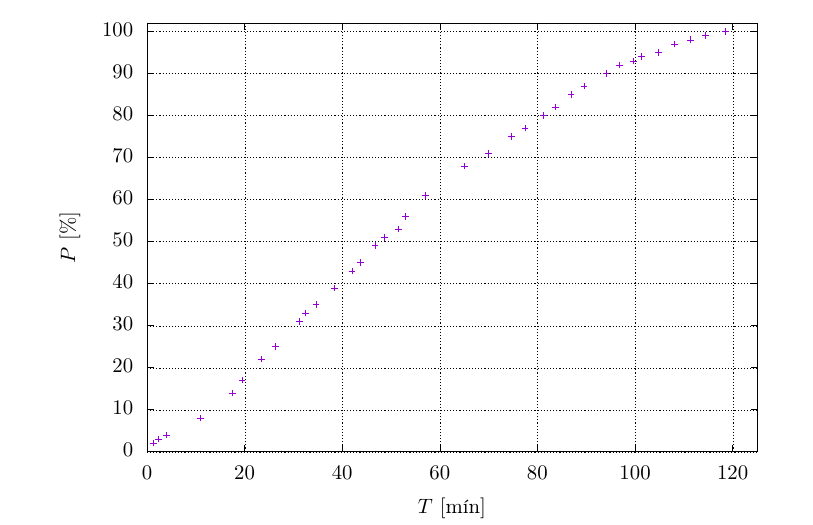
Grafið sem að við fáum beint ef við gerum graf af prósentunni sem fall af tíma lítur svona út

Líkanið sem að við erum að skoða er síðan

\[Q(t) = Q_{\text{max}}(1-e^{-t/\tau})\]

Með því að umrita jöfnuna örlítið og taka logra báðum meginn fæst síðan að

\[\log(1- P(t)) = - \frac{1}{\tau}t\]

Þar sem $P(t)=Q(t)/Q_{\text{max}}$ er í rauninni það sem að við vorum að mæla í tilrauninni, með öðrum orðum er þetta prósentan af rafhlöðunni sem fall af tíma. Takið eftir að logrinn springur þegar síminn er fullhlaðinn (því tæknilega séð nær rafhlaðan aldrei 100% hleðslu þó að síminn ljúgi að okkur og segist gera það!). Við tökum því út síðasta mælipunktinn og fáum eftirfarandi graf: