Eddington tilraunin
Er hægt að nota sólmyrkva til þess að staðfesta almennu afsæðiskenninguna?
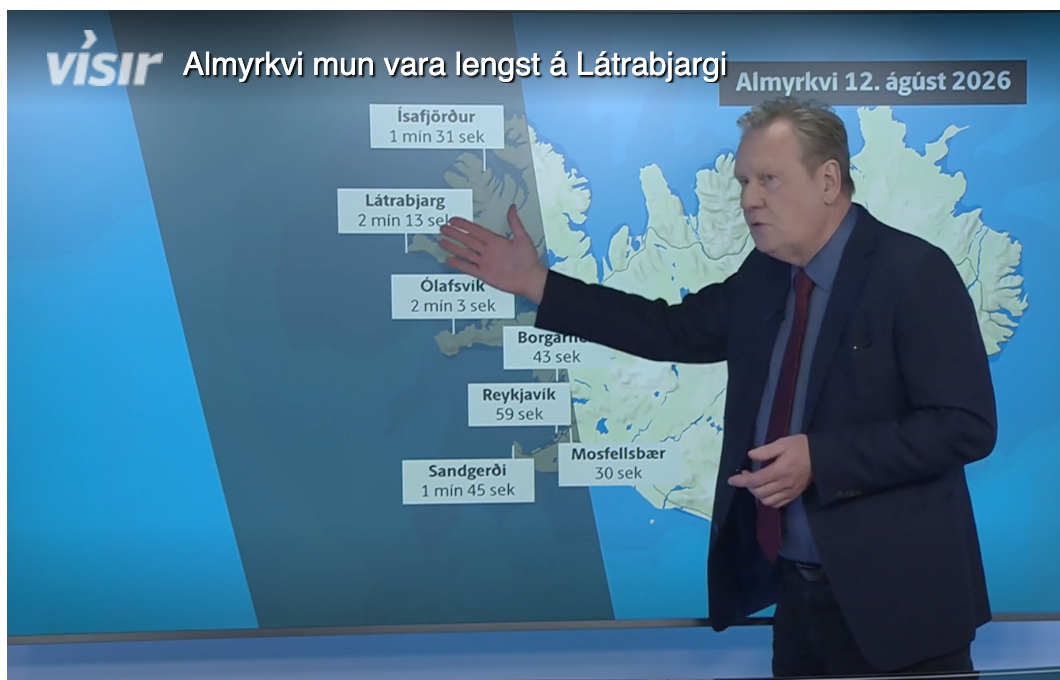
Á þrítugsafmælinu mínu, 12. ágúst 2026, verður almyrkvi á sólu. Hann mun sjást á vestanverðu landinu, meðal annars á höfuðborgarsvæðinu en í Reykjavík mun hann endast í 59 sekúndur. Besta útsýnið verður þó líklegast á Snæfelsnesinu og á Vestfjörðum. Sólmyrkvinn mun vara lengst á Látrabjargi, eða í 2 mínútur og 13 sekúndur.
Ég ætla að framkvæma Eddington tilraunina á afmælinu mínu. Það er kannski viðeigandi því að ég stunda rannsóknir á svartholum en tilvist þeirra er spáð fyrir um af almennu afstæðiskenningunni sem að Alberts Einstein setti fram árið 1915 í miðri fyrri heimsstyrjöldinni. Það þótti eftirtektarvert á þeim tíma þegar að Bretinn, Arthur Eddington, staðfesti með mælingu á sólmyrkva árið 1919, í fyrsta sinn kenningu Einsteins.
Í þessari bloggfærslu ætla ég að rekja svolítið hvaða lore liggur á bak við þessa merku tilraun, svo ætla ég að útskýra hvernig að við Stjörnu-Sævar ætlum að framkvæma þessa tilraun í sólmyrkvanum 2026. Áhugasamir sem að vilja aðstoða við að framkvæma þessa eða aðrar mælingar í sólmyrkvanum eru beðnir um að hafa samband við mig á netfangi matthias.harksen[hjá]gmail.com.
Sjá einnig: https://www.mathpages.com/rr/s6-03/6-03.htm
Svo er auðvitað David Tong búinn að gera þetta best https://www.damtp.cam.ac.uk/user/tong/gr/gr.pdf#sec1.3.5
minnast líka á John Earman, Clark Glymour í https://www.jstor.org/stable/27757471?seq=1
og upprunalegu greinina eftir Dyson, Eddington og Davidson eddington-grein.pdf sem sýnir meðal annars þetta graf:
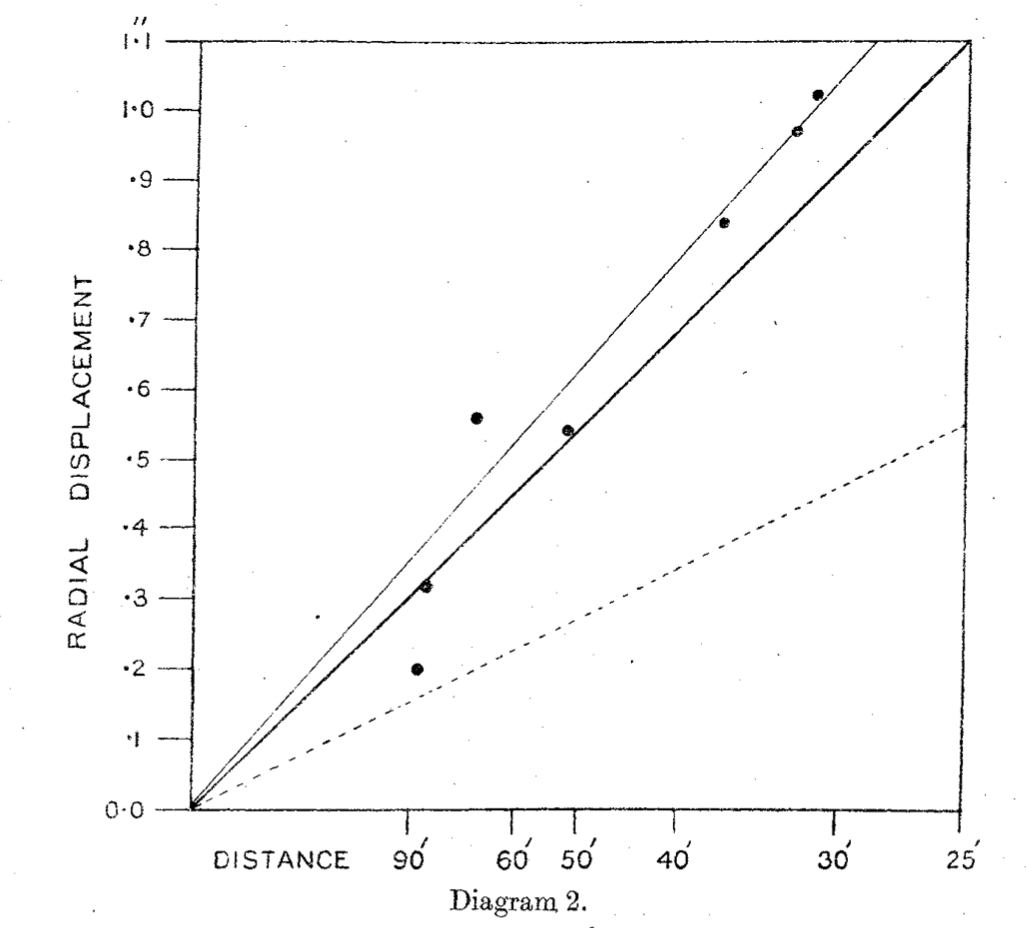Graf úr grein Eddington af tilfærslunni sem fall af fjarlægð frá sólinni sem sýnir samræmi við kenningu Einsteins frekar heldur en brotalínuna sem táknar kenningu Newtons.
Tvær Newtonskar útleiðslur á ljóssveigju
Það er engin sérstaða í því að ljós sveigi í kringum sólina. Reyndar spáir Newtonska aflfræðin einnig fyrir að ljós muni sveigja í kringum sólina. Hinsvegar munar faktor tveimur á kenningunum sem var það sem að Eddington tilraunin skar úr um til að greina hvort kenningin væri nákvæmari í þessu atriði.
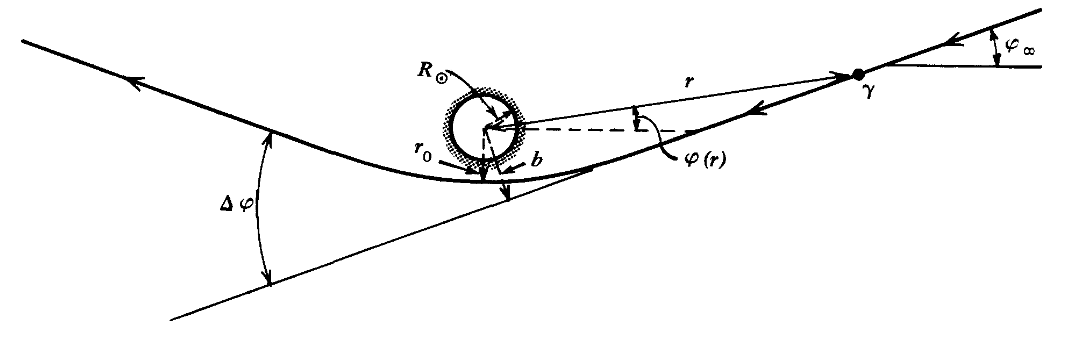
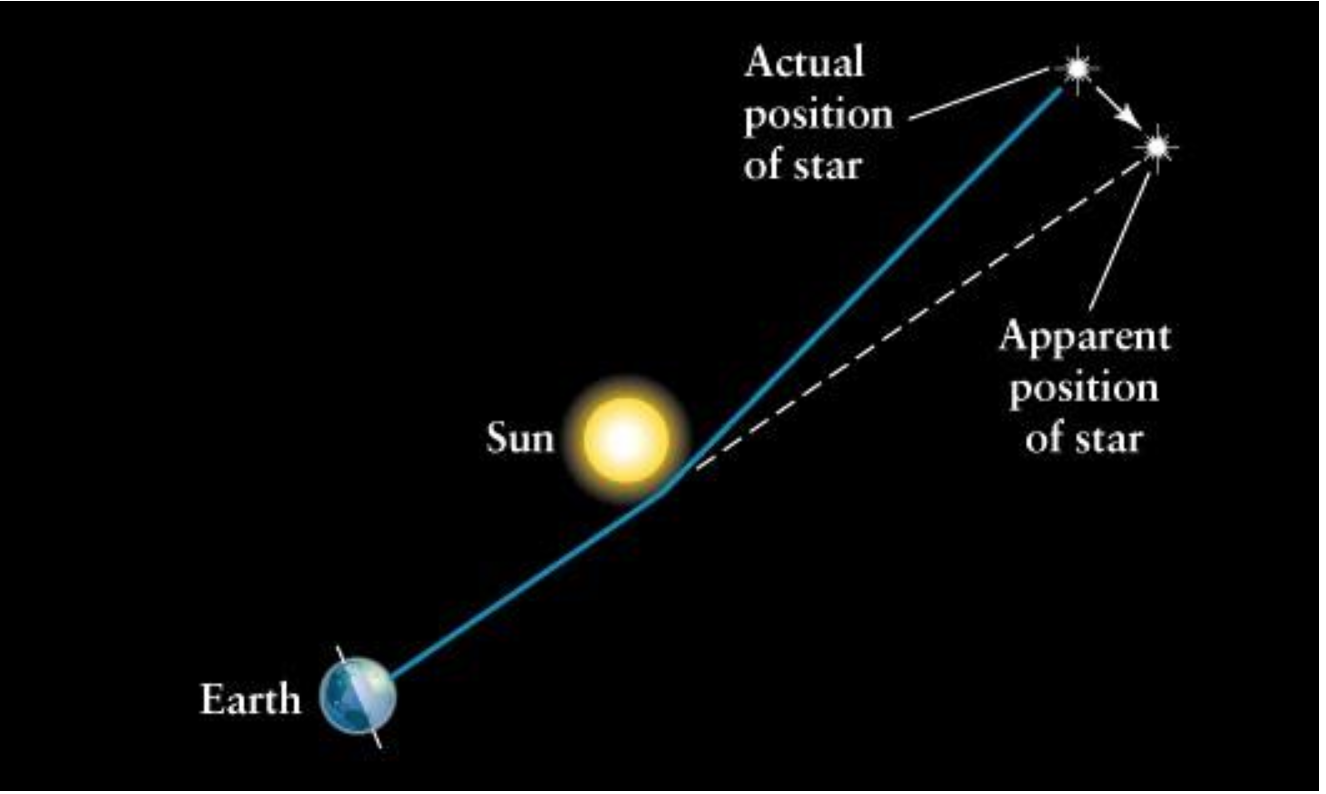Ljóssveigja í kringum massamikinn hlut. Athugandi á jörðinni sér stjörnuna færast í sólmyrkva.
Mynd eftir Weinberg
Myndin sýnir hvernig stjörnur fyrir sólmyrkvan (blátt) færast út í geislalæga stefnu og mynda rauðu dílana.
Fréttatími sem sýnir kortið.
Horfa á bíómyndina: https://www.imdb.com/title/tt0995036/
Fyrri Newtonska útleiðslan
Fyrsta útleiðslan byggir á handwavy útleiðslu eftir Stenger newtonian-deflection.pdf en því meira sem að maður rýnir í hana því fleiri vandamál koma í ljós við hana.
Lítum á ljóseind með orku $E = hf$ sem ferðast með hraða $c$ meðfram $x$-ás. Ljóseindin hefur þá virkan massa $m = \frac{E}{c^2}$ Látum massa $M \geq \frac{hf}{c^2}$ vera staðsetann í $(0,b)$ þar sem að $b$ er svokölluð kennilengd árekstrarins (e. impact parameter). Eini krafturinn sem að verkar á ljóseindina í þessu ferli er þyngdarkrafturinn. Við athugum að í punkti $(x,y)$ þá er þyngdarkrafturinn sem að verkar á ögnina með massa $m$ gefinn með:
\[\vec{F}_G = -\frac{GM \frac{hf}{c^2}}{(x^2+(b-y)^2)^{3/2}} \begin{pmatrix} x \\ y-b \end{pmatrix}\]Sem fyrsta stigs nálgun á ferlinum þá gerum við ráð fyrir að ljóseindin haldi hraða $c$ meðfram $x$-ás en það þýðir að $x = ct$ og samkvæmt keðjureglunni leyfum við okkur því að gera eftirfarandi nálgun fyrir lárétta þáttinn
\[\frac{dp_x}{dt} = \frac{dp_x}{dx} \frac{dx}{dt} = c \frac{dp_x}{dx}\]og eins fyrir lóðrétta þáttinn höfum við
\[\frac{dp_y}{dt} = \frac{dp_y}{dx} \frac{dx}{dt} = c \frac{dp_y}{dx}\]En þetta gefur því að
\[\begin{align*} \Delta p_x &= -\int_{-\infty}^{+\infty} \frac{GM \frac{hf}{c^3}x}{(x^2 + (b-y)^2)^{3/2}} dx \\ &= \left[ \frac{G M \frac{hf}{c^3}}{\sqrt{x^2 + (b-y)^2}} \right]_{x=-\infty}^{x = +\infty} = 0\,. \end{align*}\]svo að í þessari nálgun er engin breyting á skriðþunganum í lárétta stefnu. Við fáum hinsvegar að
\[\begin{align*} \Delta p_y &= \int_{-\infty}^{+\infty} \frac{GM \frac{hf}{c^3} (b-y)}{(x^2+(b-y)^2)^{3/2}} dx \\ &= \left[ \frac{GM \frac{hf}{c^3}x}{(b-y)\sqrt{x^2+(b-y)^2}} \right]_{x=-\infty}^{x=+\infty} \\ &= \frac{2 GM \frac{hf}{c^3}}{b-y} \end{align*}\]Ljóssveigjuhornið, $\psi_{\text{N}}$, má þá meta með því að velja stjörnur sem sýnast vera rétt fyrir utan disk sólarinnar þannig $b-y \approx R$ þar sem $R$ er geisli sólarinnar.
\[\psi_{\text{N}} \approx \frac{\Delta p_y}{p} = \frac{2 G M}{c^2 R} = 4{,}21 \text{ rad} = 0{,}8698\text{''}\]þ.e.a.s. rúmlega ein bogasekúnda. Þetta reynist vera helmingurinn af spágildinu samkvæmt almennu afstæðiskenningunni. Eddington tilraunin reynir því að skera úr um hvort að gildið sé nær $\psi_{\text{N}}$ eða $\psi_{\text{GR}}$.
Það er auðvelt að bæta við mati á því hversu stór áhrif tunglið hefur á niðurstöðuna. En þá fæst að
\[\psi_{\text{Tungl}} = \frac{2 G M_{\text{T}}}{c^2 R_{\text{T}}} = 0{,}000015 \psi_{N}\]þar sem að $M_T$ og $R_T$ eru massi og geisli tunglsins. Þetta sýnir að við getum hunsað áhrif tunglsins á ljóssveigjuna í Eddington tilrauninni.
Seinni Newtonska útleiðslan
Hin útleiðslan er byggð á 0508030.pdf og kampen.pdf. Fyrir ögn í sígildu miðlægu þyngdarmætti, $V(r) = -\frac{GMm}{r}$, þá er einfaldast að vinna í pólhnitum $(r,\theta)$. Það eru tvær varðveittar stærðir í þessu tilviki, annars vegar heildarorka agnarinnar, sem er þá gefin með
\[E = \frac{1}{2}m(\dot{r}^2 + r^2 \dot{\theta}^2) + V(r).\]þar sem að $\dot{r} = \frac{dr}{dt}$ og $\dot{\theta} = \frac{d\theta}{dt}$. Hin varðveitta stærðin er hverfiþungi agnarinnar (þar sem að krafturinn sem að verkar á ögnina liggur alltaf í geislalæga stefnu) sem er þá gefinn með
\[L = mr^2 \dot{\theta}.\]Við umritum nú orkuvarðveisluna með eftirfarandi hætti: við losum okkur við $\dot{\theta} = \frac{L}{mr^2}$ og við notum keðjuregluna $\frac{dr}{dt} = \frac{dr}{d\theta} \frac{d\theta}{dt} = \frac{dr}{d\theta}\dot{\theta}$, saman gefur þetta eftir smá algebru að
\[E = \frac{L^2}{2mr^4}\left( \left(\frac{dr}{d\theta}\right)^2 + r^2 \right) + V(r)\,,\]En þessa jöfnu má leysa fyrir $\frac{dr}{d\theta}$ þannig að við fáum
\[\frac{dr}{d\theta} = \frac{r^2}{L}\sqrt{2m\bigg(E + \frac{GM m}{r}\bigg) - \frac{L^2}{r^2}}\,.\]En þetta er fyrsta stigs afleiðujafna sem hefur þekkta lausn
\[r(\theta) = \frac{\ell}{1 - \epsilon \cos(\theta)}\,.\]Þar sem við skilgreindum kennistærðirnar
\[\ell = \frac{L^2}{GMm^2}\,, \hspace{0.5cm} \epsilon = \sqrt{1 + \frac{2 E L^2}{G^2 M^2 m^3}} \,.\]Hér er $\ell$ hálfur þverbrennistrengur (e. semilatus rectum) og $\epsilon$ miðvik (e. eccentricity) fyrir keilusniðið.
Nú er leikur einn að ákvarða hornið sem að ögn með upphafshraða $v_0$ og massa $m$ myndar við það að nálgast sólina með kennilengd $b$. Hér fáum við þá að
Gamalt
Það er engin sérstaða í því að ljós sveigi í kringum sólina. Reyndar spáir Newtonska aflfræðin einnig fyrir að ljós muni sveigja í kringum sólina. Hinsvegar munar faktor tveimur á kenningunum sem var það sem að Eddington tilraunin skar úr um til að greina hvort kenningin væri nákvæmari í þessu atriði.
Fyrsta útleiðslan byggir á newtonian-deflection.pdf og hin er byggð á 0508030.pdf.
Lítum á ögn með massa $m$ sem byrjar með upphafshraða $v_0$ í $x = -\infty$ og $y=0$. Látum massa $M \geq m$ vera staðsetann í $(0,b)$ þar sem að $b$ er svokölluð kennilengd árekstrarins (e. impact parameter). Eini krafturinn sem að verkar á massann $m$ í þessu ferli er þyngdarkrafturinn. Það er fræg niðurstaða eftir Newton að einu hugsanlegu ferlarnar sem koma til greina fyrir hreyfingu agnarinnar í slíku miðlægu mætti eru keilusniðin. Það fer eftir gildinu á $v_0$ hvort að hreyfingin verður sporbaugur eða breiðbogi. Við athugum að í punkti $(x,y)$ þá er þyngdarkrafturinn sem að verkar á ögnina með massa $m$ gefinn með:
\[\vec{F}_G = \frac{GMm}{(x^2+(y-b)^2)^{3/2}} \begin{pmatrix} x \\ y-b \end{pmatrix}\]En heildarkrafturinn er tengdur skriðþungabreytingunni samkvæmt $\vec{F}_{\text{heild}} = \frac{d \vec{p}}{dt} = \vec{F}_G$. Varðveislulögmálin segja okkur síðan að heildarhverfiþunginn sé varðveittur þannig að
\[mv_0 b = L = (\vec{r} \times \vec{p})_z = m(x v_y - y v_x)\]og það að heildarorkan sé varðveitt segir okkur að
\[\frac{1}{2}mv_0^2 = E = \frac{1}{2}m (v_x^2 + v_y^2) - \frac{GMm}{\sqrt{x^2+(y-b)^2}}\]Við getum litið á hverfiþungavarðveisluna og orkuvarðveisluna sem jöfnuhneppi sem leyfir okkur að ákvarða breytistærðirnar $v_x = \frac{dx}{dt}$ og $v_y = \frac{dy}{dt}$ sem fall af $x,y$. Með það í huga þá sjáum við eftir smá algebru að $v_y = \frac{1}{x}(v_0 b + v_x y)$ og með því að stinga því inn í orkujöfnuna við fáum eftirfarandi $2.$ stigs margliðu fyrir $v_x$
\[(1+\frac{y^2}{x^2})v_x^2 + \frac{2v_0 b y}{x^2} v_x + v_0^2 (\frac{b^2}{x^2}-1) - \frac{2GM}{\sqrt{x^2 + (y-b)^2}} = 0\]sem gefur því að
\[v_x = \frac{-v_0 b y \pm x v_0 \sqrt{x^2+y^2 - b^2 + \frac{2GM}{v_0^2} \frac{x^2+y^2}{\sqrt{x^2+(y-b)^2}}}}{x^2+y^2}\]En við athugum svo að með keðjureglunni má umrita lárétta þáttinn þannig að
\[F_x = \frac{dp_x}{dt} = \frac{dp_x}{dx} \frac{dx}{dt} + \frac{dp_x}{dy} \frac{dy}{dt} = \frac{dp_x}{dx}v_x + \frac{dp_x}{dy}v_y\]og eins fæst fyrir lóðrétta þáttinn
\[F_y = \frac{dp_y}{dt} = \frac{dp_y}{dx} \frac{dx}{dt} + \frac{dp_y}{dy} \frac{dy}{dt} = \frac{dp_y}{dx}v_x + \frac{dp_y}{dy}v_y\]þar sem að þættir kraftsins $F_x$ og $F_y$ eru þekktir samkvæmt þyngdarlögmálinu og $v_x$ og $v_y$ þekkt þá má nota þetta til þess að ákvarða
Ögn í sígildu miðlægu mætti
Fyrir ögn í sígildu miðlægu þyngdarmætti, $V(r) = -\frac{GMm}{r}$, þá er einfaldast að vinna í pólhnitum $(r,\theta)$. Það eru tvær varðveittar stærðir í þessu tilviki, annars vegar heildarorka agnarinnar, sem er þá gefin með
\[E = \frac{1}{2}m(\dot{r}^2 + r^2 \dot{\theta}^2) - V(r).\]þar sem að $\dot{r} = \frac{dr}{dt}$ og $\dot{\theta} = \frac{d\theta}{dt}$. Hin varðveitta stærðin er hverfiþungi agnarinnar (þar sem að krafturinn sem að verkar á ögnina liggur alltaf í geislalæga stefnu) sem er þá gefinn með
\[L = mr^2 \dot{\theta}.\]Við umritum nú orkuvarðveisluna með eftirfarandi hætti: við losum okkur við $\dot{\theta} = \frac{L}{mr^2}$ og við notum keðjuregluna $\frac{dr}{dt} = \frac{dr}{d\theta} \frac{d\theta}{dt} = \frac{dr}{d\theta}\dot{\theta}$, saman gefur þetta eftir smá algebru að
\[E = \frac{L^2}{2mr^4}\left( \left(\frac{dr}{d\theta}\right)^2 + r^2 \right) + V(r)\,,\]En þessa jöfnu má leysa fyrir $\frac{dr}{d\theta}$ þannig að við fáum
\[\frac{dr}{d\theta} = \frac{r^2}{L}\sqrt{2m\bigg(E + \frac{GM m}{r}\bigg) - \frac{L^2}{r^2}}\,.\]En þetta er fyrsta stigs afleiðujafna sem hefur þekkta lausn
\[r(\theta) = \frac{\ell}{1 - \epsilon \cos(\theta)}\,.\]Þar sem við skilgreindum kennistærðirnar
\[\ell = \frac{L^2}{GMm^2}\,, \hspace{0.5cm} \epsilon = \sqrt{1 + \frac{2 E L^2}{G^2 M^2 m^3}} \,.\]Hér er $\ell$ hálfur þverbrennistrengur (e. semilatus rectum) og $\epsilon$ miðvik (e. eccentricity) fyrir keilusniðið.
Nú er leikur einn að ákvarða hornið sem að ögn með upphafshraða $v_0$ og massa $m$ myndar við það að nálgast sólina með kennilengd $b$. Hér fáum við þá að
Forspárgildi almennu afstæðiskenningarinnar
Nú skulum við leiða út hvert gildið á horninu er samkvæmt almennu afsæðiskenningunni. Þyngdarsviðinu í kringum sólina er þar lýst með Schwarzschild-metruninni, en hún er gefin með
\[ds^2 = -(1-\frac{r_s}{r})c^2dt^2 + \frac{dr^2}{(1-\frac{r_s}{r})} + r^2 d\theta^2 + r^2 \sin^2\theta \, d\phi^2\,,\]Þar sem að við kynntum Schwarzschild-geislann $r_s = \frac{2GM}{c^2}$. Við munum einskorða okkur við $\theta = \frac{\pi}{2}$ með $\dot{\theta} = 0$. Með því að skoða hreyfijöfnur fyrir metrunina fæst að það eru tvær varðveittar stærðir, annars vegar
\[E = (1-\frac{r_s}{r})c^2 \dot{t} \, \hspace{0.5cm} L = r^2 \dot{\phi}\,.\]En þær samsvara orku og hverfiþunga eindarinnar. Fyrir ljóseind höfum við síðan að hreyfingin uppfyllir:
\[-(1-\frac{r_s}{r})c^2\dot{t}^2 + \frac{\dot{r}^2}{(1-\frac{r_s}{r})} + r^2 \dot{\phi}^2 = 0 \,,\]En með smá umritun og með því að nota varðveittu stærðirnar til að losna við $\dot{t}$ og $\dot{\phi}$ þá fáum við að
\[\frac{1}{2}\dot{r}^2 + V_{\text{eff}}(r) = \frac{E^2}{2c^2}\,,\]þar sem
\[V_{\text{eff}}(r) = \frac{L^2}{2r^2}(1-\frac{r_s}{r})\,.\]Notum svo innsetninguna $u = \frac{1}{r}$ og keðjuregluna þannig að $\frac{dr}{d\phi} = \frac{du}{d\phi} \frac{dr}{du} = - \frac{1}{u^2}\frac{du}{d\phi}$ en það gefur okkur því að
\[\left( \frac{du}{d\phi} \right)^2 + u^2(1-r_s u) = \frac{E^2}{c^2 L^2}\,.\]Þessa afleiðujöfnu er ekki hægt að leysa á lokuðu formi. Við munum því Taylor-liða fyrir $r \gg r_s$ með öðrum orðum fyrir $ u r_s \ll 1$. En það þýðir að við fáum:
\[\begin{align*} \phi &= \phi_0 + \int \frac{du}{\sqrt{\frac{E^2}{c^2L^2}- u^2(1-r_su)}} \\ &= \phi_0 + \frac{c L}{E}\int \left( 1 - \frac{c^2L^2}{E^2r_s^2}(ur_s)^2(1-ur_s) \right)^{-1/2}du \end{align*}\]